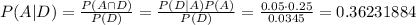Question

g Suppose a factory production line uses 3 machines, A, B, and C for making bolts. The total output from the line is distributed as follows: A produces 25%, B produces 35%, and C produces 40%. The defect rate for A is 5%, B is 4%, and C is 2%. If a bolt chosen at random is found to be defective, what is the probability that it came from machine A

Answer 1

The probability that it came from A, given that is defective is 0.362.

Explanation:

Define the events:

A: The element comes from A.

B: The element comes from B.

C: The element comes from C.

D: The elemens is defective.

We are given that P(A) = 0.25, P(B) = 0.35, P(C) = 0.4. Recall that since the element comes from only one of the machines, if an element is defective, it comes either from A, B or C. Using the probability axioms, we can calculate that

`P(D) = P(A\cap D) + P(B\cap D) + P(C\cap D)`

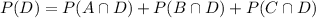
Recall that given events E,F the conditional probability of E given F is defined as

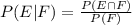`P(E|F) = (P(E\cap F))/(P(F))`, from where we deduce that

`P(E\cap F) = P(E|F)P(F)`.

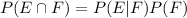We are given that given that the element is from A, the probability of being defective is 5%. That is P(D|A) =0.05. Using the previous analysis we get that

`P(D) = P(A)P(D|A)+P(B) P(D|B) + P(C)P(D|C) = 0.05\cdot 0.25+0.04\cdot 0.35+0.02\cdot 0.4 = 0.0345`

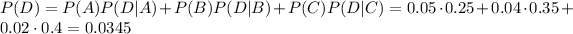
We are told to calculate P(A|D), then using the formulas we have

`P(A|D) = (P(A\cap D))/(P(D))= (P(D|A)P(A))/(P(D))= (0.05\cdot 0.25)/(0.0345)= 0.36231884`