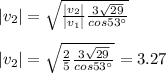Question

Se tienen 2 vectores cuyos módulos están en la misma razón que 5 y 2. Si cuando forman 53º su resultante mide 3√29u, ¿Cuánto mide el mayor vector?

Answer 1

|v2| = 3.27

Step-by-step explanation:

You have two vector v1 and v2. The relation between the magnitudes of both vectors is given by:

`(|v_1|)/(|v_2|)=(5)/(2)`

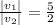
Furthermore, the projection (the dot product) of one vector on the other one is given by the following formula:

`v_1 \cdot v_2 = |v_1||v_2|cos\theta`

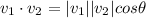
The dot product between v1 and v2 is 3√29. If you multiply the right hand side of the last equation by |v2|/|v2| you obtain:

`3√(29)=(|v_1|)/(|v_2|)|v_2|^2cos(53\°)`

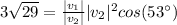
you do |v2| the subject of the formula:

`|v_2|=\sqrt)(3√(29))/(cos53\°)\\\\|v_2|=\sqrt{(2)/(5)(3√(29))/(cos53\°)}=3.27`