Answer:
(C)x=11.6, y=23.2
Explanation:
Using Theorem of Intersecting Secant and Tangent
Applying this theorem in the diagram, we have:
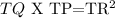
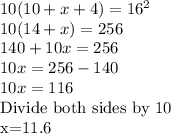
Next, we apply Theorem of Intersecting Chords
PV X VQ=SV X VR
4 X x= 2 X y
Recall earlier we got: x=11.6
2y=4 X 11.6
2y=46.4
Divide both sides by 2
y=46.4/2=23.2
Therefore: x=11.6, y=23.2