Question

When a cannon balls fired the equation of his pathway can be modeled by h= -16t^2 + 128t

find the maximum height of the cannonball and find a time it will take for the cannonball to reach the ground

Answer 1

The maximum height of the cannonball 'h' = 256

The time will take for the cannonball to reach the ground 't' =4

Step-by-step explanation:

Step-by-step explanation:-

The given equation h(t) = -16 t² + 128 t ...(i)

Differentiating equation(i) with respective to 't' we get

`h^(l) (t) = (dh)/(dt) = -16 (2 t) +128 (1)`

`h^(l) (t) = -16 (2 t) +128 (1) = 0`

`-32 t +128 = 0`

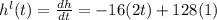
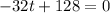
- 32 t = -128

t = 4

Now

Again differentiating with respective to 'x'

`h^(ll) (t) = (d^(2) h)/(dt^(2) ) = -16 (2 ) < 0`

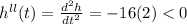
The function is Maximum at t = 4

The maximum value

h(t) =-16 t² + 128 t

h(4) = - 16 (4)² + 128(4) = 256

Conclusion:-

The maximum height of the cannonball 'h' = 256

The time will take for the cannonball to reach the ground 't' =4