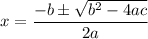Answer:
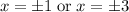
Explanation:
Substitute
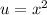 into the equation. This will make the quadratic formula easy to use.
into the equation. This will make the quadratic formula easy to use.
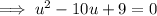
Consider the form
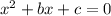 . Find a pair of integers whose product is
. Find a pair of integers whose product is
 and whose sum is
and whose sum is
 . In this case, whose product is
. In this case, whose product is
 and whose sum is
and whose sum is
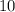 . And write the factored form using the integers.
. And write the factored form using the integers.
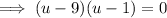
If any individual factor on the left side of the equation is equal to
 , the entire expression will be equal to
, the entire expression will be equal to
 .
.
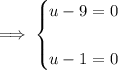
Set
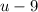 equal to
equal to
 and solve for
and solve for
 . Similarly, Set
. Similarly, Set
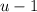 equal to
equal to
 and solve for
and solve for
 .
.
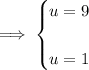
Substitute the real value of
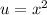 back into the solved equation.
back into the solved equation.
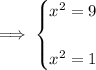
Take the square root of both sides of the equations to eliminate the exponent on the left side.

Solve both the equations for the value of
 .
.
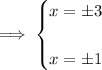
Hence, this is our required solution for this question.

Additional information:
There are three ways to solve a quadratic equation:
- Factoring
- Complete the Square
- Quadratic Formula
Factoring uses the logic that the product of any number and zero is zero. Complete the square method uses square root, and the quadratic formula is the simpler method of it.
Quadratic Formula