Question

A plant produces aluminum, facing costs of C(A) = \frac{A^2}{10}, where A is the number of aluminum units produced, and selling them on the competitive market for a price \$ 30. A farmer grows beets next to the aluminum factory, facing costs of C(B) = 5B + \frac{B^2}{100} + \frac{A^2}{20}, where B is the number of beets produced, and selling them for \$ 15 on the competitive market. Because aluminum pollution is harmful to agricultural production, the state government imposes a tax on aluminum production. What is the socially optimal tax on aluminum?

Answer 1

$10

Step-by-step explanation:

We are to account for external costs in production, since we are asked to find optimal tax.

Given:

`C(A) = (A^2)/(10)`

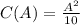
We now have:

`C(A) = (A^2)/(10) + (A^2)/(20)`

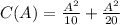
A represents number of aluminum units produced, let's find A, since the margnal cost is $30.

Thus,

`30 = (A)/(5) + (A)/(10)`

`30 = (2A + A)/(10)`

`300 = 3A`

`A = (300)/(3)`

`A = 100`

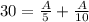
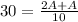
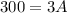
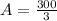
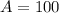
Let's equate the private marginal cost with the marginal revenue of each unit in order to achieve this amount of produced units with tax, t.

We have:

`30 - t = (A)/(5)`

Substituting 100 for A above, we have:

`30 - t = (100)/(5)`

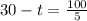
30 - t = 20

t = 30 - 20

t = 10

Therefore, the socially optimal tax on aluminum is $10 per unit