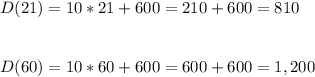Answer:
Day 21: 810 m
Day 60: 1,200 m
Explanation:
The amount of meters she walk everyday can be modeled as a linear function, as the rate of variation is a constant (10 m/day):
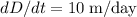
This constant (10 m/day) is the slope of the linear function.
We know one point of the linear function (D(20)=800) and the slope, so we can calculate the y-intercept:
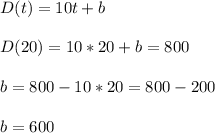
Now, we can calculate the distance she walks by day 21 and day 60: