Question

Solve the 3x3 system shown below. Enter the values of x, y, and z.

x+2y-x=-3

2x-y+z=5

x-y+z=4

Answer 1

Answer: x=1 y=-1 z=2

Explanation:

Answer 2

x = 1

y = -1

z = 2

Explanation:

You have the following system of equations:

`x+2y-z=-3\ \ \ \ \ (1)\\\\2x-y+z=5\ \ \ \ \ \ (2)\\\\x-y+z=4\ \ \ \ \ (3)`

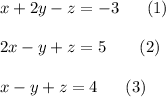
First, you can subtract euqation (3) to equation (1):

x + 2y - z = -3

-x +y -z = - 4

0 3y -2z = -7 (4)

Next, you can multiply equation (3) by 2 and subtract it to equation (2):

2[ x -y + z = 4]

-2x +y -z = -5

0 -y + z= 3 (5)

You multiply equation (5) by 2 and sum (5) with (4):

2[ -y + z = 3]

3y -2z= -7

y + 0 = -1

Then y = -1

Next, you replace y=-1 in (5) to obtain z:

-(-1) + z = 3

z = 2

Finally, you can replace z and y in the equation (3) to obtain x:

x - (-1) + (2) = 4

x = 1