Question

Solve the equation in the interval from 510^\circ510 ∘ 510, degrees to 1050^\circ1050 ∘ 1050, degrees. Your answer should be in degrees. \sin(x)=0sin(x)=0

Answer 1

540°, 720° and 900°

Explanation:

Given equation sin(x) = 0 lying between the interval 510°≤x≤1050°. To find the value of x within this range, we first find the value of from the equation as shown;

sin(x) = 0

taking the arcsin of both sides;

`sin^(-1)(sinx) = sin^(-1) 0\\x = 0^(0)`

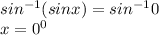
Since x is positive in the first and second quadrant, in the second quadrant, the value of x will be 180°-0° = 180°

Subsequent value of x equivalent to 0° will be addition of 180° to each previous value gotten. The values of x within the range given are as shown

x1 =0°

x2 = 180°-0° = 180(2nd quadrant)

x3 = 180°+180° = 360°

x4 = 360°+180° = 540°

x5 = 540°+180°=720°

x6 = 720°+180° = 900°

x7 = 900°+180° = 1080°

We can see from the values above that the values of x that falls within the given range are 540°, 720° and 900°. This gives the required answers in degrees.