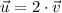Question

State if the two vectors are parallel, orthogonal, or neither.

u=18i+8j

v=9i+4j

Answer 1

Parallel, since
`\vec u = 2\cdot \vec v`.

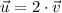Explanation:

The relation between both vectors is determined by the use of the dot product, whose expression is:

`\cos \theta = (\vec u \bullet \vec v)/(\|\vec u\| \|\vec v\|)`

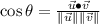
Where:

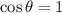`\cos \theta = 1` if vectors are parallel to each other and
`\cos \theta = 0` if vectors are orthogonal. Then, norms and dot product are calculated hereafter:

`\|\vec u\| = \sqrt{18^(2)+8^(2)}`

`\|\vec u\| \approx 19.698`

`\|\vec v \| = \sqrt{9^(2)+4^(2)}`

`\|\vec v\| \approx 9.849`

`\vec u \bullet \vec v = (18)\cdot (9) + (8)\cdot (4)`

`\vec u \bullet \vec v = 194`

`\cos \theta = (194)/((19.698)\cdot (9.849))`

`\cos \theta = 1`

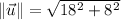
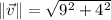
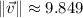
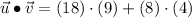
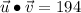
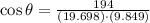
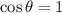
The two vectors are parallel to each other, which is also supported by the fact that one vector is multiply of the other one. That is,

`18i + 8j = 2\cdot (9i + 4j)`

`\vec u = 2\cdot \vec v`