Answer:
It will take 1.12 seconds for the hammer to reach the ground.
Explanation:
The height of the hammer after t seconds is given by the following equation:
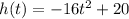
How long will it take the hammer to reach the ground?
This is t for which h(t) = 0. So
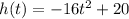

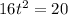
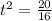
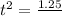
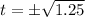
Time is a positive measure, so
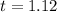
It will take 1.12 seconds for the hammer to reach the ground.