Question

Someone help please:

A vendor at a street fair sells popcorn in cones, all of height 9 inches. The

sharing-size cone has 3 times the radius of the skinny-size cone. About how

many times more popcorn does the sharing cone hold than the skinny cone?

Answer 1

The sharing cone holds about 9 times more popcorn than the skinny cone.

Explanation:

Cone volume:

`V = (\pi r^(2)h)/(3)`

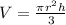
r is the radius and h is the inches.

Skinny-size cone:

Radius is r, height h. So

`V_(sk) = (\pi r^(2)h)/(3)`

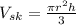
Sharing size:

Radius is now 3r. So

`V_(sh) = (\pi (3r)^(2)h)/(3) = (9\pi r^(2)h)/(3) = 3\pi r^(2)h`

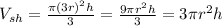
How many times more popcorn?

`r = (V_(sh))/(V_(sk)) = (3\pi r^(2)h)/((\pi r^(2)h)/(3)) = (3*3\pi r^(2)h)/(\pi r^(2)h) = 9`

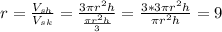
The sharing cone holds about 9 times more popcorn than the skinny cone.