Answer:
The regression line predicts that at x = 4, y equals 2143
Explanation:
Given that when x equals 4, log(y) will equal 3.331
To find: Find y when x equals 4
Since we have given that,
When x = 4,
log y = 3.331
We need to find the value of 'y' when x = 4
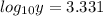
Since it is logarithmic function with base 10, Raise to power of 10 on both sides,
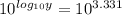
we get
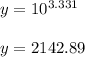
rounding to nearest whole number, we get 2143