Question

1) How many liters of carbon dioxide gas will be produced at 32°C and 747 mmHg if 1.595 kg of calcium carbonate decomposes? (calcium oxide is the other product)

2) If 175.0mL of a 2.12M potassium chloride solution is mixed with 95.0mL of a 5.97M lead (II) nitrate solution, how many grams of precipitate will be produced in this reaction?

Answer 1

1.
`V_(CO_2)=405.85L`

2.
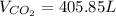
`m_(PbCl_2)=51.6gPbCl_2`

Step-by-step explanation:

Hello,

1) In this case, the reaction is:

`CaCO_3\rightarrow CaO+CO_2`

Thus, since 1.595 kg of calcium carbonate, whose molar mass is 100 g/mol, is decomposed, the following moles of carbon dioxide are produced:

`n_(CO_2)=1.595kgCaCO_3*(1000gCaCO_3)/(1kgCaCO_3)*(1molCaCO_3)/(100gCaCO_3) *(1molCO_2)/(1molCaCO_3) \\\\n_(CO_2)=15.95molCO_2`

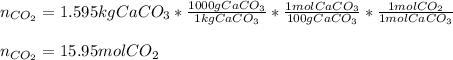
Then, by using the ideal gas equation we can compute the volume of carbon dioxide:

`V_(CO_2)=(n_(CO_2)RT)/(P)=(15.95molCO_2*0.082(atm*L)/(mol*K)*(32+273)K)/(747mmHg*(1atm)/(760mmHg) ) \\\\V_(CO_2)=405.85L`

2) In this case, the reaction is:

`2KCl(aq)+Pb(NO_3)_2(aq)\rightarrow PbCl_2(s)+2KNO_3(aq)`

Thus, lead (II) chloride is the precipitate. In such a way, we first identify the limiting reactant by firstly computing the moles of potassium chloride and lead (II) nitrate with the volumes and the molarities:

`n_(KCl)=2.12mol/L*0.175L=0.371molKCl\\n_(Pb(NO_3)_2)=5.97mol/L*0.095L=0.567molPb(NO_3)_2`

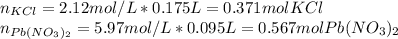
Next, we compute the moles of potassium chloride consumed by 0.567 moles of lead (II) nitrate by using their 2:1 molar ratio:

`n_(KCl)^(consumed\ by\ Pb(NO_3)_2)=0.567molPb(NO_3)_2*(2molKCl)/(1molPb(NO_3)_2)=1.134molKCl`

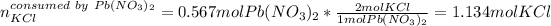
Therefore, as just 0.371 moles of potassium chloride are available we say it is the limiting reactant, for that reason, the grams of lead (II) chloride, whose molar mass is 278.1 g/mol, precipitate finally result:

`m_(PbCl_2)=0.371molKCl*(1molPbCl_2)/(2molKCl)*(278.1gPbCl_2)/(1molPbCl_2) \\\\m_(PbCl_2)=51.6gPbCl_2`

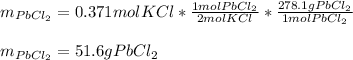
Best regards.