Question

What is the range of the function f(x)=3x^2+12x + 18

Answer 1

Answer: {y∈R: y≤6} or [6,∞)

Step-by-step explanation:

This problem doesn't require too much math. If you look at the equation given, you can see that it is a quadratic equation in the form of
`y=Ax^2+Bx+C`. Since this is a quadratic equation, we have an idea of that the graph would look like. It either curves up or down. Since this is a positive equation,
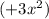`(+3x^2)`, we know that this is going to curve up. In order to find the minimum of the curve, you would use
`(-b)/(2a)`.

`(-12)/(2(3))=-2`

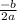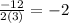
This means the x value of the parabola is -2. To find the y, you plug -2 into the original equation.

`f(2)=3(-2)^2+12(-2)+18`

`f(2)=6`

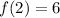
Now that we know the y value of the minimum/vertex is 6, and it is determined that the parabola curves up, the range is y≤6 because the range starts at 6 and goes off toward infinity.