Question

A sector with an area of 48\pi cm^(2) has a radius of 16 cm. what is the central angle measure of the sector in radians

Answer 1

The central angle is = 3/8 π

Explanation:

To calculate the area of the sector, we will follow the steps below;

First write down the formula for calculating the area of a sector.

If angle Ф is measured in degree, then

area of sector = Ф/360 × πr²

but if angle Ф is measured in radians, then

area of sector = 1/2 × r² × Ф

In this case, since we are asked to find the central angle measure of the sector in radians, then we will use the second formula

area = 48π cm² and radius = 16 cm

area of sector = 1/2 × r² × Ф

48π = 1/2 × 16² × Ф

48π = 1/2 ×256 × Ф

48π = 128×Ф

Divide both-side of the equation by 128

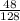`(48)/(128)` π = Ф

Ф =
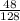`(48)/(128)` π

The right-hand side can be reduced to its lowest term

Ф = 48 ÷ 16 / 128 ÷16 π

Ф = 3/8 π