Question

A cobalt-60 source with activity 2.60×10-4 Ci is embedded in a tumor that has

mas 0.20 kg. The source emits gamma photons with average energy 1.25 MeV.
Half the photons are absorbed in the tumor, and half escape.
i. What energy is delivered to the tumor per second? [4 marks]
ii. What absorbed dose, in rad, is delivered per second? [2 marks]
iii. What equivalent dose, in rem, is delivered per second if the RBE for
these gamma rays is 0.70? [2 marks]
Page 6 of 7
iv. What exposure time is required for an equivalent dose of 200 rem? [2
marks]
B. A laser with power output of 2.0 mW at a wavelength of 400 nm is projected
onto a Calcium metal. The binding energy is 2.31 eV.
i. How many electrons per second are ejected? [6 marks]
ii. What power is carried away by the electrons? [4 marks]
C. A hypodermic needle of diameter 1.19 mm and length 50 mm is used to
withdraw blood from a patient? How long would it take for 500 ml of blood to be
taken? Assume a blood viscosity of 0.0027 Pa.s and a pressure in the vein of
1,900 Pa. [10 marks]
D. A person with lymphoma receives a dose of 35 gray in the form of gamma
radiation during a course of radiotherapy. Most of this dose is absorbed in 18
grams of cancerous lymphatic tissue.
i. How much energy is absorbed by the cancerous tissue? [2 marks]
ii. If this treatment consists of five 15-minute sessions per week over the
course of 5 weeks and just one percent of the gamma photons in the
gamma ray beam are absorbed, what is the power of the gamma ray
beam? [4 marks]
iii. If the gamma ray beam consists of just 0.5 percent of the photons
emitted by the gamma source, each of which has an energy of 0.03
MeV, what is the activity, in Curies, of the gamma ray source? [4 marks]
E. A water heater that is connected across the terminals of a 15.0 V power supply
is able to heat 250 ml of water from room temperature of 25°C to boiling point
in 45.0 secs. What is the resistance of the heater? The density of water is 1,000
kg/m2 and the specific heat capacity of water is 4,200 J/kg/°C. [10 marks]

Answer 1

A i. E = 9.62 × 10⁻⁷ J/s

ii. The absorbed dose is 4.81 × 10⁻⁶ Gy

iii. The equivalent dose is 3.37 × 10⁻⁴ rem/s

iv. t = 593471.81 seconds

B. i. 4.025 × 10¹⁵/s

ii. 0.512 mW

C. 7218092.2 seconds

D. i. 6.3 × 10⁻¹ J

ii. 1.4 × 10⁻² W

iii. 1.57 × 10³ Curie

E. 0.129 Ω

Step-by-step explanation:

The given parameters are;

Mass of tumor = 0.20 kg

Activity of Cobalt-60 = 2.60 × 10⁻⁴ Ci

Photon energy = 1.25 MeV

(i) The energy, E, delivered to the tumor is given by the relation;

`E = (1)/(2)\left (Number \, of \, decay / seconds \right )* \left (Energy \, of \, photon \right )`

`E = (1)/(2)\left (2.6* 10^(-4)Ci )* \left ((3.70* 10^(10)decays/s)/(1 Ci) \right )* 1.25* 10^(6)eV* (1.6* 10^(-19)J)/(1eV)`

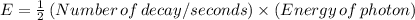
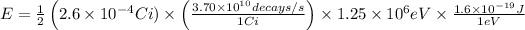
E = 9.62 × 10⁻⁷ J/s

(ii) The equation for absorbed dose is given as follows;

Absorbed dose, D, in Grays Gy = (Energy Absorbed Joules J)/Mass kg

Therefore, absorbed dose = (9.62 × 10⁻⁷ J/s)/( kg) = 4.81 × 10⁻⁶ Gy

1 Gray = 100 rad

4.81 × 10⁻⁷ Gy = 100 × 4.81 × 10⁻⁶ = 4.81 × 10⁻⁴ rad/s

(iii) Equivalent dose, H, is given by the relation;

H = D × Radiation factor,
`w_R`

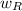
∴ H = 0.7 × 4.81 × 10⁻⁴ rad/s = 3.37 × 10⁻⁴ Sv = 3.37 × 10⁻⁴ rem/s

(iv) The exposure time required for an equivalent dose of 200 rem is given as follows;

`\dot{H} = (H)/(t)`

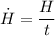
Therefore;

`t= \frac{200}{{3.37 * 10^(-4)} } = 593471.81 \, s`

∴ t = 6.9 days

B. The number of electrons ejected is given by the relation;

`N = (P)/(E) = (P * \lambda)/(hc)`

`N = (2.0 * 10^(-3) * 400 * 10^(-9))/(6.626 * 10^(-34) * 3 * 10^8) = 4.025 * 10^(15)/s`

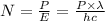
(ii) The power carried by the electron

The energy carried away by the electrons is given by the relation;

`KE_e = hv - \Phi`

`KE_e = (6.626 * 10^(-34) * 3 * 10^8)/(400 * 10^(-9)) - 2.31 * (1.6 * 10 ^(-19) )/(1)`

`KE_e = 4.9695 * 10^(-19) - 3.696 * 10 ^(-19) = 1.2735 * 10^(-19) J`

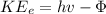
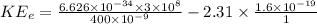
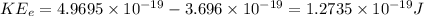
Power, P
`_e`, carried away by the electron = 4.025 × 10¹⁵ × 1.2735 × 10⁻¹⁹ = 0.512 mW

C. The given parameters are;

d = 1.19 mm, ∴ r = 1.19/2 = 0.595 × 10⁻³ m

l = 50 mm = 5 × 10⁻³ m

V = 500 ml = 5 × 10⁻⁴ m³

η = 0.0027 Pa

p = 1,900 Pa.

`(V)/(t) = (\pi )/(8) * (P/l)/(\eta ) * r^4`

`t = (8* \eta* V* l )/(\pi * P * r^4)`

`t = (8* 0.0027 * 5 * 10^(-4) * 5 * 10^(-2) )/(\pi * 1900 * (0.595 * 10^(-4) )^4)`

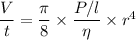
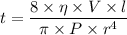
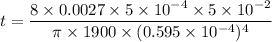
t = 7218092.2 seconds

D) i. Energy absorbed is given by the relation;

E = m×D

Where:

D = 35 Gray = 35 J/kg

m = 18 g = 18 × 10⁻³ kg

∴ E = 35 × 18 × 10⁻³ = 6.3 × 10⁻¹ J

ii. Total time for treatment = 15 × 5 = 75 minutes

Energy absorbed = 6.3 × 10⁻¹ × 100 = 63 J

Power = Energy(in Joules)/Time (in seconds)

∴ Power = 63/(75×60) = 1.4 × 10⁻² W

iii. Whereby the power is provided by 0.5% of the photons emitted by the source, we have;

`P_(source)= (P_(beam))/(0.005) =(0.0014)/(0.005) =0.28 \, W`

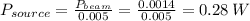
1 MeV = 1.60218 × 10⁻¹³ J

0.03 MeV = 0.03 × 1.60218 × 10⁻¹³ J = 4.80654 × 10⁻¹⁵ J/photon

Therefore, the number of disintegration per second = 0.28 J/s ÷ 4.80654 × 10⁻¹⁵ J/photon = 5.83 × 10¹³ disintegrations per second

1 Curie = 3.7 × 10¹⁰ disintegrations per second

Hence, 5.83 × 10¹³ disintegrations per second = (5.83 × 10¹³)/(3.7 × 10¹⁰) Curie

= 1.57 × 10³ Curie

E. The parameters given are;

Density of water = 1000 kg/m³

Volume of water = 250 ml = 0.00025 m³

Initial temperature, T₁, = 25°C

Final temperature, T₂, = 100°C

Change in temperature, ΔT = 100 - 25 = 75°

Specific heat capacity of the water = 4200 J/kg/°C

Mass of water = Density × Volume = 1000 × 0.00025 = 0.25 kg

∴ Heat supplied = 4200 × 0.25 × 75 = 78,750 J

Time to heat the water = 45.0 sec

Therefore, power = Energy/time = 78750/45 = 1750 W

The formula for electrical power = I²R =VI = V²/R

Therefore, where V = 15.0 V, we have;

15²/R = 1750

R = 15²/1750 = 0.129 Ω.

The resistance of the heater = 0.129 Ω.