Question

Trisomy 18 (T18) is a rare genetic disorder that severely disrupts a baby's development prior to birth. Many die before birth and most die before their first birthday. T18 occurs in only 1 in 2500 pregnancies in the U.S. A genetic test on the mother's blood can be done to test for T18 in her baby. The overall probability of a positive test result is 0.010384. The probability of a positive test result for a baby with T18 is 0.97. The probability of a negative test result for a baby without T18 is 0.99. A mother's blood tests positive for T18. What is the probability that her baby has T18

Answer 1

3.74% probability that her baby has T18

Explanation:

Bayes Theorem:

Two events, A and B.

`P(B|A) = (P(B)*P(A|B))/(P(A))`

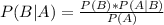
In which P(B|A) is the probability of B happening when A has happened and P(A|B) is the probability of A happening when B has happened.

In this question:

Event A: Positive test.

Event B: The baby having T18.

T18 occurs in only 1 in 2500 pregnancies in the U.S.

This means that
`P(B) = (1)/(2500) = 0.0004`

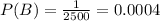
The probability of a positive test result for a baby with T18 is 0.97.

This means that
`P(A|B) = 0.97`

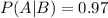
The overall probability of a positive test result is 0.010384.

This means that
`P(A) = 0.010384`

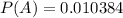
What is the probability that her baby has T18

`P(B|A) = (0.0004*0.97)/(0.010384) = 0.0374`

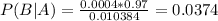
3.74% probability that her baby has T18