Question

Sean tossed a coin off a bridge into the stream below. The path of the coin can be represented by the equation 2 h tt = − 16t^2+ 72t+ 100 (where t is time in seconds and h is height in feet) How long will it take the coin to reach the stream?

Answer 1

It will take 5.61 seconds for the coin to reach the stream.

Explanation:

The height of the coin, after t seconds, is given by the following equation:

`h(t) = -16t^(2) + 72t + 100`

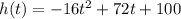
How long will it take the coin to reach the stream?

The stream is the ground level.

So the coin reaches the stream when h(t) = 0.

`h(t) = -16t^(2) + 72t + 100`

`-16t^(2) + 72t + 100 = 0`

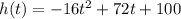
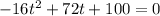
Multiplying by (-1)

`16t^(2) - 72t - 100 = 0`

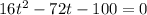
Solving a quadratic equation:

Given a second order polynomial expressed by the following equation:

`ax^(2) + bx + c, a\\eq0`.

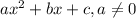This polynomial has roots
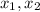`x_(1), x_(2)` such that
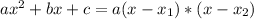`ax^(2) + bx + c = a(x - x_(1))*(x - x_(2))`, given by the following formulas:

`x_(1) = (-b + √(\bigtriangleup))/(2*a)`

`x_(2) = (-b - √(\bigtriangleup))/(2*a)`

`\bigtriangleup = b^(2) - 4ac`

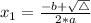
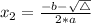
In this question:

`16t^(2) - 72t - 100 = 0`

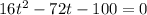
So

`a = 16, b = -72, c = -100`

`\bigtriangleup = (-72)^(2) - 4*16*(-100) = 11584`

`t_(1) = (-(-72) + √(11584))/(2*16) = 5.61`

`t_(2) = (-(-72) - √(11584))/(2*16) = -1.11`

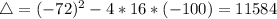
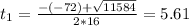
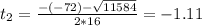
Time is a positive measure, so we take the positive value.

It will take 5.61 seconds for the coin to reach the stream.