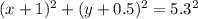The coordinates below are the endpoints of the diameter. Find the coordinates of the center Find the length of the radius. Write the equation of the circle standard form.

Question

asked May 28, 2021 129k views

1 Answer

Florentino · Answer 1 · 2021-06-01T17:30:54+0000

Answer:

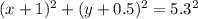
(x+1)^(2) +(y+0.5)^(2) =5.3^(2)

Explanation:

The endpoints of the diameter are (-5,3) and (3,-4).

We know that the mid point of the diameter is the center of the circle, and half of its length is the radius. Let's find the center first.

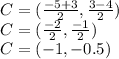
$C=((-5+3)/(2) ,(3-4)/(2) )\\C=((-2)/(2) ,(-1)/(2) )\\C=(-1, -0.5)$

The length of the diameter can be found with the formula below

$d=\sqrt{(y_(2) -y_(1) )^(2)+(x_(2) -x_(1) )^(2) } \\d=\sqrt{(-4-3)^(2) +(3-(-5))^(2) } =√(49+64)\\ d=√(113) \approx 10.6$

Therefore, the diameter is 10.6 units, approximately.

So, the radius is

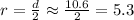
$r=(d)/(2) \approx (10.6)/(2)=5.3$

Therefore, the radius is 5.3 units.

Now we can find the equation of the circle

(x+1)^(2) +(y+0.5)^(2) =5.3^(2)