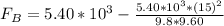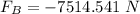Question

An amusement park ride consists of a car moving in a vertical circle on the end of a rigid boom of negligible mass. The combined weight of the car and riders is 5.40 kN, and the radius of the circle is 9.60 m. At the top of the circle, (a) what is the force FB on the car from the boom (using the minus sign for downward direction) if the car's speed is v

Answer 1

Complete Question

An amusement park ride consists of a car moving in a vertical circle on the end of a rigid boom of negligible mass. The combined weight of the car and riders is 5.40 kN, and the radius of the circle is 9.60 m. At the top of the circle,

(a) what is the force FB on the car from the boom (using the minus sign for downward direction) if the car's speed is v = 5.10 m/s?

(b) What is FB if v = 15.0 m/s? Use g=9.80 m/s2.

Answer:

The force FB at v= 5.10 m/s is
`F_B = 3.91\ kN`

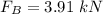
The force FB at v=15.0 m/s is
`F_B = -7514.541 \ N`

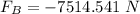
Step-by-step explanation:

The diagram of this setup is shown on the first uploaded image

From the question we are told that

The weight of the car and the rider is
`W_t = 5.40 \ kN`

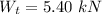
The radius of the circle is
`r = 9.80 \ m`

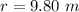
At the top the force acting on the car can be mathematically represented as

`mg -F_B = (mv^2)/(r)`

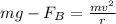
Where
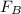`F_B` is normal upward force acting on the car , v is the linear velocity acting on the car , m is the mass of the (car+riders) , g is the acceleration due to gravity

making
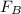`F_B` the subject we have

`F_B = m g - (mv^2)/(r)`

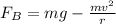
This equation can be modified to

`F_B = m g - (mgv^2)/(gr)`

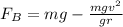
Which is equivalent to the previous equation

So

`F_B = W_t - (W_t * v^2)/(gr)`

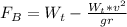
Now at
`v = 5.10 \ m/s`

`F_B = 5.40*10^(3) - (5.40 *10^(3) * (5.10)^2)/(9.8 * 9.60)`

`F_B = 3.91\ kN`

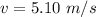
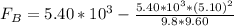
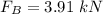
Now at
`v = 15 m/s`

`F_B = 5.40*10^(3) - (5.40 *10^(3) * (15)^2)/(9.8 * 9.60)`

`F_B = -7514.541 \ N`