Question

Solve question 3 for
41 points

Answer 1

(2)

Explanation:

Our logarithmic expression is:
`ln((√(e) )/(y^3) )`.

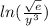Remember the logarithmic property that ln(a/b) = lna - lnb. So, we can write this as:

`ln((√(e) )/(y^3) )=ln(√(e) )-ln(y^3)`

Also, we can write square roots as powers of one-half, so √e =
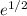`e^(1/2)`. There's another log property that:
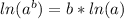`ln(a^b)=b*ln(a)`. We can apply that here for both the √e and the y³:

`ln(√(e) )-ln(y^3)=(1)/(2) ln(e)-3ln(y)`

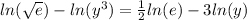
Finally, note that ln(e) is just 1, so we have:

`(1)/(2) ln(e)-3ln(y)=(1)/(2) -3ln(y)=(1-6ln(y))/(2)`

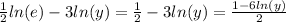
The answer is thus (2).

~ an aesthetics lover