Question

A phone company offers two monthly plans. Plan A costs $25 plus an additional $0.07 for each minute of calls. Plan B costs $16 plus an additional $0.09 for each minute of calls. Q1: For what amount of calling do the two plans cost the same? Q2: What is the cost when the two plans cost the same?

Answer 1

1) For 450 minutes of calling the two plans cost the same.

2) The cost when the two plans cost the same is $56.5.

Explanation:

The cost of both plans can be modeled by linear functions.

Plan A:

$25 plus an additional $0.07 for each minute of calls.

So, for t minutes of calls, the cost is:

`A(t) = 25 + 0.07t`

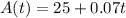
Plan B:

$16 plus an additional $0.09 for each minute of calls.

So, for t minutes of calls, the cost is:

`B(t) = 16 + 0.09t`

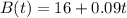
Q1: For what amount of calling do the two plans cost the same?

This is t for which:

`A(t) = B(t)`

`25 + 0.07t = 16 + 0.09t`

`0.02t = 9`

`t = (9)/(0.02)`

`t = 450`

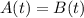
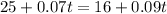
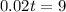
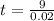
For 450 minutes of calling the two plans cost the same.

Q2: What is the cost when the two plans cost the same?

This is A(450) or B(450), since they are the same.

`B(450) = 16 + 0.09*450 = 56.5`

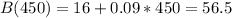
The cost when the two plans cost the same is $56.5.