Answer:
Terry had a finish time with a z-score of -1.45.
Jane had a finish time with a z-score of -2.12. Due to the lower z-score, Jane had the more convincing win.
Explanation:
Z-score:
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question:
Whoever's z-score was lower, that is, took less time to complete the race compared to their competitors, had the more convincing win.
Terry:
The mean finish time for a yearly amateur auto race was 185.53 minutes with a standard deviation of 0.339 minute. The winning car, driven by Terry, finished in 185.04 minutes.
This means that

So



Terry had a finish time with a z-score of -1.45.
Jane:
The previous year's race had a mean finishing time of 111.6 with a standard deviation of 0.104 minute. The winning car that year, driven by Jane, finished in 111.38 minutes.
This means that
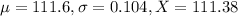
So

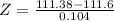

Jane had a finish time with a z-score of -2.12. Due to the lower z-score, Jane had the more convincing win.