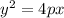Question

The parabola opens to the right. The focus is given as

F (p,0) and directrix x = -p. The distance between the

focus and point P is equal to the distance between the

directrex and point P. Continue to simplify the equation to

solve for y2. THE ANSWER IS 4px!! :)

Answer 1

y^2 = 4px

Explanation:

edg 2021

Answer 2

Explanation:

We have that the focus is at (p,0) and that the directrix is x=-p. Take the point (-p,0) of the directrix. We know that the vertex of the parabola is at the middle point ot the line segment that joins the points (p,0) and (-p,0). To get the middle piont, we take the average coordinate by coordinate. That is, the middle point is
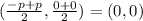`((-p+p)/(2), (0+0)/(2)) = (0,0)`. The general formula of a parabola of vertex (h,k) that opens to the right or to the left is given by

`(y-k)^2 = 4p(x-h)`

Where |p| is the distance from the focus to the vertex. If the parabola opens to the right, then p>0 and p<0 otherwise. In our case, h =0=k, so we get that

`y^2 = 4px`