Answer:
The solution to the equation are

Both of his values are positive real numbers
Explanation:
The general formula of a quadratic equation is expressed as
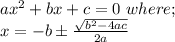
Given the expression 0 = x² – 5x – 4 which can be rewritten as shown below;
x² – 5x – 4 = 0
Comparing this to the general equation; a = 1, b = -5, c= -4
To get the solution to the quadratic equation, we will use the general formula above;

Both of his values are positive real numbers