Answer:
0.5584 probability that she succeeds at 10 or more free-throws in a sample of 12 free-throws.
Explanation:
For each free throw, there are only two possible outcomes. Either she makes it, or she does not. The probability of making a free throw is independent of other free throws. So we use the binomial probability distribution to solve this question.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.
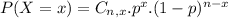
In which
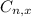 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
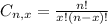
And p is the probability of X happening.
The probability that Shruti succeeds at any given free-throw is 80%, percent.
This means that
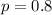
Sample of 12 free throws:
This means that

Use her results to estimate the probability that she succeeds at 10 or more free-throws in a sample of 12 free-throws.
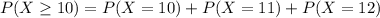
In which
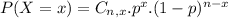
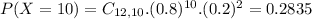
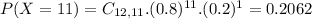
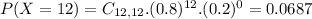
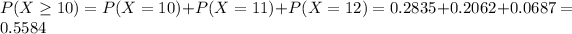
0.5584 probability that she succeeds at 10 or more free-throws in a sample of 12 free-throws.