Answer:
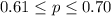
And for this case we can estimate the proportion of households who recycle paper is given by:
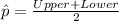
And replacing we got:
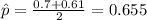
And for this case the answer is 0.655 for the proportion of households who recycle paper
Explanation:
For this case we know that the confidence interval for the proportion of interest is given by:
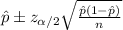
And for this case the confidence interval is given:
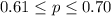
And for this case we can estimate the proportion of households who recycle paper is given by:
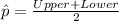
And replacing we got:
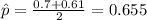
And for this case the answer is 0.655 for the proportion of households who recycle paper