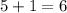Answer: 6
Explanation:

Let's begin by converting the repeating decimal to a fraction and then to a mixed number.
Take the number:
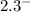
Let x (our result) be equal to that number.

Multiply by 1 followed by as many zeros as repeating decimals; in this case 1. Therefore, 10.
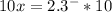
This basically moves the decimal point one number to the right and since we have infinite 3's, we simply move 1 three and add another.
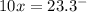
Subtract this and the original equation (
 )
)
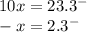
-----------------
10 - 1 = 9 and we have the same infinite repeating number 3, therefore they cancel out, leaving 23-2 = 21
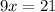
Divide by 9
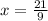
Simplify by 3.
21/3=7
9/3=3
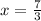
Now, convert to a mixed number. To do this, divide.
7/3=2
6
-------
1
The 2 is the whole number, 1 is the numerator and 3 the denominator.
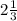
------------------------------------------------------------------------------------------------
Now we can solve this;

Add the whole numbers and the fractions separately.
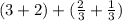
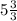
3 and 3 can be simplied.
3/3=1
3/3=1
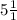
The result is 1, add this to the 5.