Answer:
a) The range of scores that includes the middle 95% of these test scores is between 470 and 674.
b) The range of scores that includes the middle 90% of these test scores is between 488.1 and 655.9.
Explanation:
68-95-99.7 rule:
The Empirical Rule states that, for a normally distributed random variable:
68% of the measures are within 1 standard deviation of the mean.
95% of the measures are within 2 standard deviation of the mean.
99.7% of the measures are within 3 standard deviations of the mean.
In this problem, we have that:
Z-score:
Problems of normally distributed samples are solved using the z-score formula.
In a set with mean
 and standard deviation
and standard deviation
 , the zscore of a measure X is given by:
, the zscore of a measure X is given by:

The Z-score measures how many standard deviations the measure is from the mean. After finding the Z-score, we look at the z-score table and find the p-value associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X. Subtracting 1 by the pvalue, we get the probability that the value of the measure is greater than X.
In this question:
Mean
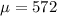 , standard deviation
, standard deviation

a. Use the 68-95-99.7 rule to estimate the range of scores that includes the middle 95% of these test scores.
By the 68-95-99.7 rule, within 2 standard deviations of the mean.
572 - 2*51 = 470
572 + 2*51 = 674
The range of scores that includes the middle 95% of these test scores is between 470 and 674.
b. Use technology to estimate the range of scores that includes the middle 90% of these test scores.
Using the z-score formula.
Between these following percentiles:
50 - (90/2) = 5th percentile
50 + (90/2) = 95th percentile.
5th percentile.
X when Z has a pvalue of 0.05. So when X when Z = -1.645.

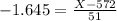
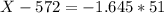
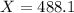
95th percentile.
X when Z has a pvalue of 0.95. So when X when Z = 1.645.

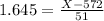

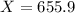
The range of scores that includes the middle 90% of these test scores is between 488.1 and 655.9.