Question

Find the mean, median, and mode(s) of the data. Choose the measure that best represents the data. Explain your reasoning. Find the mean, median, and mode(s) of the data with and without the outlier. Which measure did the outlier affect the most? 8, 10, 10, 11, 16, 17, 19, 21, 41

Answer 1

Replacing we got:

`\bar X = 17`

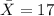
The median for this case since the sampe size of n = 9 is the value in the 5th position from the dataset ordered on increasing way and we got:

`Median = 16`

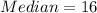
The mode for this case is the most reapeated value and we got:

`Mode= 10`

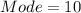
For this case we can use the median as the best measure since is resistant to any possible outliers from the dataset.

If we consider 41 as an outlier (since the distance for this value from the mean is too big compared with the rest of the values) we can find the new statistics and we got:

`\bar X = 14`

`Median = (11+16)/(2)= 13.5`

`Mode= 10`

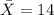
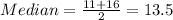
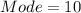
The mode for this case is not affected for the outlier

Explanation:

We have the following data given:

8, 10, 10, 11, 16, 17, 19, 21, 41

We can estimate the mean with this formula:

`\bar X = (\sum_(i=1)^n X_i)/(n)`

Replacing we got:

`\bar X = 17`

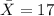
The median for this case since the sampe size of n = 9 is the value in the 5th position from the dataset ordered on increasing way and we got:

`Median = 16`

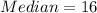
The mode for this case is the most reapeated value and we got:

`Mode= 10`

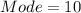
For this case we can use the median as the best measure since is resistant to any possible outliers from the dataset.

If we consider 41 as an outlier (since the distance for this value from the mean is too big compared with the rest of the values) we can find the new statistics and we got:

`\bar X = 14`

`Median = (11+16)/(2)= 13.5`

`Mode= 10`

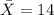
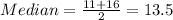
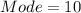
The mode for this case is not affected for the outlier