Question

To which interval would we restrict f(x) = cos (x-π/4) so that f(x) is invertible?

Answer 1

The range of x values for which y is unique is 2·π

Explanation:

For a function j: X → Y to be invertible, we have that for every y in Y, there is associated only one x which is an element of x

Hence, f(x) = cos(x - π/4) gives

the x intercept at two penultimate points of the graph of cos(x - π/4) are;

x = 2.36, and x = 8.64

x = 3/4·π, and x = 2.75·π =
`2\tfrac{3}{4}\cdot \pi`

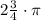
Hence the range of x values for which y is unique is presented as follows

`2\tfrac{3}{4}\cdot \pi - (3)/(4)\cdot \pi = 2}\cdot \pi`

The range of x values for which y is unique = 2·π.