Question

The initial number of bacteria in the dish was 1,150. The amount of bacteria doubles at the end of each hour. Write a function b(t) that would represent this relationship after t hours. Use this function to determine how many bacteria would be in the dish after 10 hours and write it only as a number without units.

Answer 1

`B(t) = 1150*(2)^(t)`

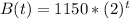
After 10 hours: 1,177,600

Explanation:

The number of bacteria after b hours is given by the following equation:

`B(t) = B(0)(1+r)^(t)`

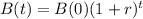
In which B(0) is the initial number of bacteria and r is the rate that it increases.

The initial number of bacteria in the dish was 1,150. The amount of bacteria doubles at the end of each hour.

This means that
`B(0) = 1150, B(1) = 2*1150`

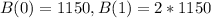
So

`B(t) = B(0)(1+r)^(t)`

`2*1150 = 1150(1+r)^(1)`

`1 + r = 2`

`r = 1`

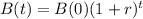
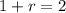
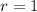
So

`B(t) = 1150*(2)^(t)`

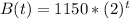
After 10 hours:

`B(10) = 1150*(2)^(10) = 1177600`

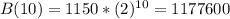
1,177,600 bacteria after 10 hours.