Answer:
4 terms
Degree of the 4th term = 5
Coefficient of the 2nd term = -6
Degree of the polynomial = 11
Explanation:
Terms of polynomials: parts of the expression that are separated by the addition or subtraction operation.
Therefore, there are 4 terms in this polynomial.
If a term of the polynomial has more than one variable, then to calculate the degree of that term, add the powers of all the variables in the term.
Therefore, the degree of the fourth term is:
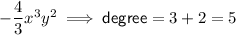
The coefficient is the constant. Therefore, the coefficient of the second term is -6
Degree of a polynomial: The greatest exponent of a variable in the polynomial equation.
As some of the terms in this polynomial have more than one variable, we must first calculate the degrees of the individual terms, and then select the greatest as the degree of the polynomial equation.
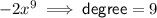
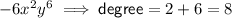

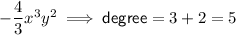
Therefore, the greatest degree is 11, so this is the degree of the polynomial.