Question

Two terms of an arithmetic sequence are $a_{12}=70$a12​=70​ and A sub 30 is equal to 124$a_{30}=124$a30​=124​ . Write an explicit rule for the n$n$n​ th term

Answer 1

Tn = 34+3n

Explanation:

The formula for finding the nth term of an arithmetic sequence is expressed as shown;

`Tn = a+(n-1)d`

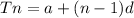
a is the first term of the sequence

n is the number of terms

d is the common difference

If T₁₂ = 70 and T₃₀ = 124

T₁₂ = a+(12-1)d = 70

T₁₂ = a+11d = 70... (1)

Similarly;

T₃₀ = a + (30-1)d = 124

T₃₀ = a +29d = 124...(2)

Solving equation 1 and 2 simultaneously to get a and d.

Subtracting 2 from 1 we have;

29d - 11d = 124-70

18d = 54

d = 54/18

d = 3

Substituting d = 3 into equation 1 to get a we have;

a + 11(3) = 70

a + 33 = 70

a = 70-33

a = 37

The explicit rule for the nth term of the sequence can be gotten by substituting the value of a and d into the formula Tn = a+(n-1)d

Tn = 37+(n-1)*3

Tn = 37+3n-3

Tn = 34+3n