Question

Use the ratio test to determine whether the series is convergent or divergent.2 +4/2^2 + 8/3^2 + 16/4^2 +

Answer 1

The result is 2 > 1. Hence, the series diverges

Explanation:

You have the following series:

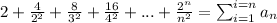`2+(4)/(2^2)+(8)/(3^2)+(16)/(4^2)+...+(2^n)/(n^2)=\sum_(i=1)^(i=n)a_n` (1)

You use the ratio test to determine if the series is convergent or divergent. The ratios test is given by:

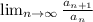`\lim_(n \to \infty) (a_(n+1))/(a_n)` (2)

Then, you replace the series (1) in (2):

`\lim_(n \to \infty) ((2^(n+1))/((n+1)^2))/((2^n)/(n^2))= \lim_(n \to \infty) ((2^n2)(n^2))/(2^n(n+1)^2)\\\\\lim_(n \to \infty) (2n^2)/(n^2+2n+1)= \lim_(n \to \infty) (2n^2)/(n^2[1+(2)/(n)+(1)/(n^2)]) \\\\\lim_(n \to \infty) (2)/(1+(2)/(n)+(1)/(n^2))=(2)/(1+0+0)=2`

In the ratio test you have that if the limit is greater than 1, the series diverges.

The result is 2 > 1. Hence, the series diverges.