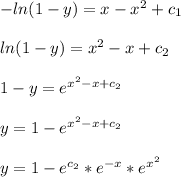Solve dy/dx = (1-x)(1-y)

Question

asked Feb 24, 2021 154k views

1 Answer

Achiash · Answer 1 · 2021-03-01T02:12:09+0000

Answer:

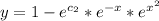
$y=1-e^{c_(2)}}*e^(-x) *e^(x^2)$

Explanation:

We begin with the differential equation
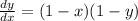
(dy)/(dx) =(1-x)(1-y)

Firstly, we need to get the
and
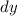as well as the
and
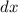on the same sides as each other

To do this, we can multiply each side by
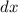and divide each side by
(1-y)

Doing this will give us the following differential

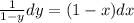
(1)/(1-y) dy=(1-x)dx

Now, we can integrate each side

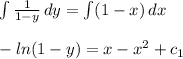
$\int\limits(1)/(1-y) \, dy =\int (1-x) \, dx\\\\-ln(1-y)=x-x^2+c_(1)$

Now, we need to solve for y

$-ln(1-y)=x-x^2+c_(1)\\\\ln(1-y)=x^2-x+c_(2) \\\\1-y=e^{x^2-x+c_(2)} \\\\y=1-e^{x^2-x+c_(2)}\\\\y=1-e^{c_(2)}}*e^(-x) *e^(x^2)$