Answer:
4. two real solutions
Explanation:
 (Given)
(Given)
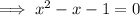
- Equating it with

- We find: a = 1, b = -1, c = -1
- Next, we calculate the discriminant of the given quadratic equation by plugging the values of a, b and c in the formula

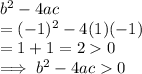
-> Given quadratic equation has two real solutions.