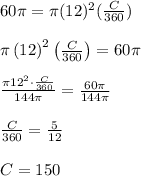Question

A sector with a radius 12 cm has an area of 60 pi cm2. What is the central angle measure of the sector in degrees?

Answer 1

Answer:5pi/6

Explanation:

Answer 2

The central angle measure of the sector is 150º.

Explanation:

A sector of a circle is the portion of a circle enclosed by two radii and an arc.

When you know the central angle the area of a sector is given by

`A=\pi r^2((C)/(360) )`

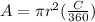
where

r is the radius of the circle of which the sector is part.

C is the central angle in degrees.

We know that the area of the sector is
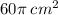`60\pi \:cm^2` and the radius is 12 cm. Applying the above formula and solving for the central angle we get that

`60\pi =\pi (12)^2((C)/(360)) \\\\\pi \left(12\right)^2\left((C)/(360)\right)=60\pi \\\\(\pi 12^2\cdot (C)/(360))/(144\pi )=(60\pi )/(144\pi )\\\\(C)/(360)=(5)/(12)\\\\C=150`