Answer:
Please, read the answer below.
Explanation:
You have the following function:

(a) To find the intervals of increase or decrease of f(x) you first calculate the derivative of f(x):
![(df)/(dx)=(d)/(dx)[12x^4-4x^2+5]\\\\(df)/(dx)=12(4)x^3-4(2)x=48x^3-8x](https://img.qammunity.org/2021/formulas/mathematics/college/wjfjp8dwb3d9yz3p2xii8kcagxdvy0dy8v.png) (2)
(2)
Next, you equal the derivative to zero and obtain the roots of the obtained polynomial:
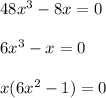
Then, you have the following roots for x:
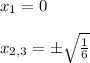 = ±0.40
= ±0.40
Hence, there are three special points.
Next, you evaluate the derivative (expression (2)) for the x values close to the x1, x2 and x3. The values of the derivative give to us the value of the slope of a tangent line in that point, and so, if the function increases or decreases:
First interval, for a number lower than -0.40
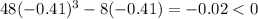
The function decreases in the interval:
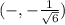
It is necessary that after x=-0.40 the function increases until the next special point, that is x=0. Then, the interval in which the function increases is:
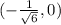
By symmetry, from the point x=0 until x=0.40 the function decreases.
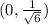
Next, you evaluate the expression (2) for a number higher than 0.40:
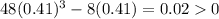
Then, the function increases for the following interval:
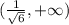
(b) Due to the results obtained in the previous step you can conclude that the local minimum are:
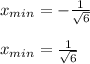
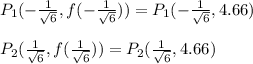
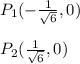
(these are the point in which the function change of a decrease to an increase)
The same reason as before. There in one local maximum:
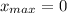
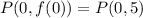
(c) The inflection points are calculated by using the second derivative:
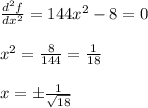
Then , there are two inflection points , given by:
