Question

In a survey of students, 1162 stated they cheated and 2468 stated they did not. If one student is randomly selected what is the probability that they cheated

Answer 1

`n = 1162 +2468 =3630`

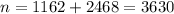
And the probability that they cheated and we can use the classical definition of probability given by:

`p =(successes)/(Total)`

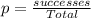
And replacing we got:

`p=(1162)/(3630)= 0.320`

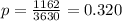
So then the probability of people cheated is 0.320 or 32% approximately

Explanation:

For this problem we know that in a survey of students, 1162 stated they cheated and 2468 stated they did not.

The total of people is given by:

`n = 1162 +2468 =3630`

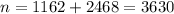
And the probability that they cheated and we can use the classical definition of probability given by:

`p =(successes)/(Total)`

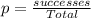
And replacing we got:

`p=(1162)/(3630)= 0.320`

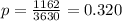
So then the probability of people cheated is 0.320 or 32% approximately