1 Answer

Srivani · Answer 1 · 2021-11-03T13:53:08+0000

Answer:

$(7\pi)/(4)$ .

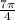Explanation:

Given information:

Radius of circle = 8 cm

Area of sector =
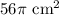
$56\pi\text{ cm}^2$

Formula for area of sector is

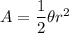
$A=(1)/(2)\theta r^2$

where, r is radius and
$\theta$ is central angle in radian.

Substitute
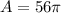$A=56\pi$ and r=8 in the above formula.

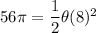
$56\pi=(1)/(2)\theta (8)^2$

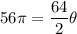
$56\pi=(64)/(2)\theta$

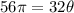
$56\pi=32\theta$

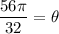
$(56\pi)/(32)=\theta$

$(7\pi)/(4)=\theta$

Therefore, the measure of the sector in radians is
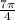$(7\pi)/(4)$ .

Please log in or register to add a comment.