Question

Element X decays radioactively with a half-life of 14 minutes if there are 680 grams of element X how long to the nearest 10th of a minute would it take the element to decay 17 grams

Answer 1

It would take 74.5 minutes for the element to decay 17 grams.

Explanation:

The amount of element X after t minutes is given by the follwoing equation:

`X(t) = X(0)e^(rt)`

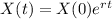
In which X(0) is the initial amount of the substance and r is the decay rate.

Half life of 14 minutes.

This means that
`X(14) = 0.5X(0)`

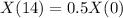
So

`X(t) = X(0)e^(rt)`

`0.5X(0) = X(0)e^(14r)`

`e^(14r) = 0.5`

`\ln{e^(14r)} = ln(0.5)`

`14r = ln(0.5)`

`r = (ln(0.5))/(14)`

`r = -0.0495`

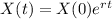
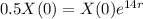
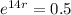
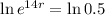
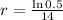
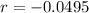
So

`X(t) = X(0)e^(-0.0495t)`

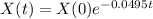
There are 680 grams of element X

This means that
`X(0) = 680`

`X(t) = X(0)e^(-0.0495t)`

`X(t) = 680e^(-0.0495t)`

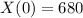
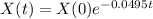
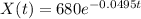
How long would it take the element to decay 17 grams

This is t for which X(t) = 17. So

`X(t) = 680e^(-0.0495t)`

`17 = 680e^(-0.0495t)`

`e^(-0.0495t) = (17)/(680)`

`e^(-0.0495t) = 0.025`

`\ln{e^(-0.0495t)} = ln(0.025)`

`-0.0495t = ln(0.025)`

`0.0495t = -ln(0.025)`

`t = -(ln(0.025))/(0.0495)`

`t = 74.5`

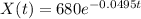
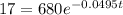
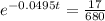
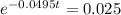
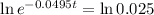
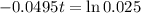
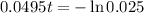
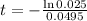
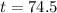
It would take 74.5 minutes for the element to decay 17 grams.