Question

En la reacción I2(g) + Br2(g) « 2 IBr(g), Keq = 280 a 150°C. Suponga que se permite que 0.500 mol de IBr en un matraz de 1.00 L alcancen el equilibrio a 150°C. ¿Cuáles son las presiones parciales de equilibrio de IBr, I2 y Br2?

Answer 1

`p_(I_2)=0.926atm\\p_(Br_2)=0.926atm\\p_(IBr)=15.5atm`

Step-by-step explanation:

Hello,

In this case, given the initial load of 0.500 mol of IBr in the 1.00-L, we compute its initial concentration:

`[IBr]_0=(0.500mol)/(1.00L)=0.500M`

Hence, by knowing the original reaction, we should invert it as IBr will produce iodine and bromine considering the initial load:

`2IBr(g)\rightleftharpoons I_2(g) + Br_2(g)`

Therefore, the equilibrium constant should be inverted:

`K'=(1)/(Keq)=(1)/(280)=3.57x10^(-3)`

So we write the law of mass action:

`K'=([I_2][Br_2])/([IBr]^2)`

That in terms of the change
`x` due to the reaction extent turns out:
`3.57x10^(-3)=((x)(x))/((0.500-2x)^2)`

In such a way, solving by using solver or quadratic equation we obtain:

`x_1=-0.0339M\\x_2=0.0267M`

Clearly, the solution is 0.0267M, thus, the equilibrium concentrations are:

`[I_2]=x=0.0267M`

`[Br_2]=x=0.0267M`

`[IBr]=0.5M-2x=0.5M-2*0.0267M=0.447M`

Thus, with the given temperature (150+273.15=423.15K), we compute the partial pressures by using the ideal gas equation:

`p_(I_2)=[I_2]RT=0.0267(mol)/(L) *0.082(atm*L)/(mol*K)*423.15K\\\\p_(I_2)=0.926atm\\\\p_(Br_2)=[Br_2]RT=0.0267(mol)/(L) *0.082(atm*L)/(mol*K)*423.15K\\\\p_(Br_2)=0.926atm\\\\p_(IBr)=[IBr]RT=0.447(mol)/(L) *0.082(atm*L)/(mol*K)*423.15K\\\\p_(IBr)=15.5atm`

Best regards.

Answer 2

P IBr: 15.454atm

I₂: 0.923 atm

P Br₂: 0.923atm

Step-by-step explanation:

Basados en la reacción:

I₂(g) + Br₂(g) ⇄ 2 IBr(g)

La constante de equilibrio, Keq, es definida como:

`Keq = (P_(IBr)^2)/(P_(I_2)P_(Br_2))`

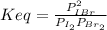
Se cumple la relación de Keq = 280 cuando las presiones están en equilibrio

Usando PV = nRT, la presión inicial de IBr es:

P = nRT / V; 0.500mol*0.082atmL/molK*423.15K / 1.00L = 17.3 atm

Siendo las presiones en equilibrio:

P IBr: 17.3 - 2X

P I₂: X

P Br₂: X

Donde X representa el avance de reacción.

Remplazando en Keq:

280 = (17.3 - 2X)² / X²

280X² = 4X² - 69.2X + 299.29

0 = -276X² - 69.2X + 299.29

Resolviendo para X:

X = -1.174 → Solución falsa. No existen presiones negativas

X = 0.923 → Solución real

Así, las presiones parciales en equilibrio de cada compuesto son:

P IBr: 17.3 - 2X = 15.454atm

P I₂: X = 0.923atm

P Br₂: X = 0.923atm