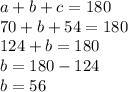Question

The sum of the three numbers is 180. The first number is 10 more than the mean of the three numbers and the second number is 4 less than the mean. What is the third number?

Answer 1

The third number (c) is 54.

The other ones are 70 and 56.

Explanation:

We have 3 numbers, let's call them a, b and c.

We know that the sum of the three numbers is 180, thus:

`a+b+c=180`

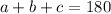
We also know that the first number is 10 more than the mean of the three numbers (Note: the mean is the sum of the numbers divided by the number of numbers). Thus:

`a=(a+b+c)/(3) +10\\a=(a+b+c+30)/(3) \\3a=a+b+c+30\\2a=b+c+30`

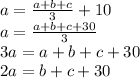
Finally the second number is 4 less than the mean:

`b=(a+b+c)/(3)-4\\b=(a+b+c-12)/(3) \\3b=a+b+c-12\\2b=a+c-12`

Now we have our set of equations and we can proceed to solve them:

`a+b+c=180\\2a=b+c+30\\2b=a+c-12`

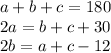
Solving for a in our first equation we have:
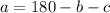`a=180-b-c` and substituting this in our second equation we have:

`2a=b+c+30\\2(180-b-c)=b+c+30\\360-2b-2c=b+c+30\\330=3b+3c\\110=b+c`

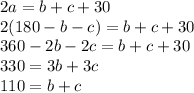
Now taking this last result into our first equation we have:

`a+b+c=180\\a+(b+c)=180\\a+110=180\\a=70`

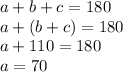
Now we are going to solve for b in our second equation and substitute this in our third equation:
`b= 180-a-c`

`2b=a+c-12\\2(180-a-c)=a+c-12\\360-2a-2c=a+c-12\\372=3a+3c\\124=a+c`

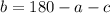
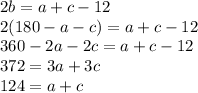
But we know that a =70, so we can substitute it in our last line:

`124=a+c\\124=70+c\\54=c`

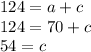
Now we just need to find b and we can use our first original equation to do this:

`a+b+c=180\\70+b+54=180\\124+b=180\\b=180-124\\b=56`