Question

Aretha is driving her car 325 miles to get to her vacation home. She travels the first 195 miles in 3 hours. At this rate, how long will it take her to make the complete trip

Answer 1

Answer: 5 hours

Explanation:

An easy way to find the answer is to make an equation.

`(195)/(3) =(325)/(x)`

Make a diagonal oval with the two known numbers. So for this equation, it is 325×3. After multiplying, you will get a product of 975. Then divide this by the 3rd known number, which in our case is 195. 975÷195=5.

I hope you learned from this and don't hesitate to ask if you have any questions.

Answer 2

For this case we know that the total distance to travel is 325 mi. And we know that Aretha travels at the following velocity:

`V = (X)/(t) = (195 mi)/(3 hr)= 65 (mi)/(hr)`

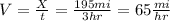
Then we can use the following definition:

`D = Vt`

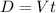
Where D is the distance and V the velocity. And solving for t we got:

`t = (D)/(V)`

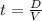
And replacing we got:

`t = (325 mi)/(65 (mi)/(hr))= 5`

So then we can conclude that after 5 hours at this rate Aretha will arrive to home

Explanation:

For this case we know that the total distance to travel is 325 mi. And we know that Aretha travels at the following velocity:

`V = (X)/(t) = (195 mi)/(3 hr)= 65 (mi)/(hr)`

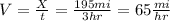
Then we can use the following definition:

`D = Vt`

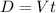
Where D is the distance and V the velocity. And solving for t we got:

`t = (D)/(V)`

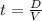
And replacing we got:

`t = (325 mi)/(65 (mi)/(hr))= 5`

So then we can conclude that after 5 hours at this rate Aretha will arrive to home