Question

Eric, Cam, and Brooke are playing a game of mini golf on a computer. The computer program for the game stores

objects in terms of x and y coordinates. All coordinate values are in meters.

The players are shooting at the hole, which is located at (3,2). After hitting their initial shots, Eric's golf ball is at

(-6,6), Cam's golf ball is at (8,-6), and Brooke's golf ball is at (10,8).

If the player whose ball is farthest from the hole should shoot next, which player should shoot next?

Answer 1

Answer: Erick

Step-by-step explanation: 9.85

Answer 2

Eric

Explanation:

First, we determine the distance of each player to the hole using the distance formula.

Given points
`(x_1,y_1)$ and (x_2,y_2)`

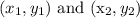
Distance
`=√((x_2-x_1)^2+(y_2-y_1)^2)`

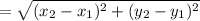
Eric

The hole is at (3,2)

Eric's golf ball is at point (-6,6)

Distance=
`√((-6-3)^2+(6-2)^2)`

`=√((-9)^2+(4)^2)\\=√(97) \\\approx 9.85`

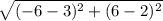
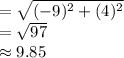
Cam

The hole is at (3,2)

Cam's golf ball is at point (8,-6)

Distance=
`√((8-3)^2+(-6-2)^2)`

`=√((5)^2+(-8)^2)\\=√(89) \approx9.43`

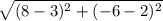
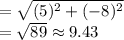
Brooke

The hole is at (3,2)

Brooke's golf ball is at point (10,8)

`Distance=√((10-3)^2+(8-2)^2)\\=√((7)^2+(6)^2)\\=√(85) \approx 9.22`

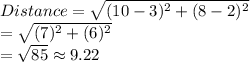
Since Eric's ball is the farthest from the hole, Eric should shoot next.