Answer:
None of the options represent the right answer. (Real answer:
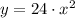 )
)
Explanation:
The parabola shown above is vertical and least distance between focus and directrix is equal to
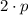 . Then, the value of p is determined with the help of the Pythagorean Theorem:
. Then, the value of p is determined with the help of the Pythagorean Theorem:
![2\cdot p = \sqrt{(0-0)^(2)+[6-(-6)]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/bjqh5y16d796pienewwb9u5i7r0m7r2ksz.png)
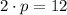
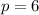
The general equation of a parabola centered at (h,k) is:
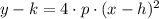
It is evident that parabola is centered at origin. Hence, the equation of the parabola in standard form is:
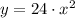
None of the options represent the right answer.