Question

Find the solutions for a triangle with a = 16, c =12, and B = 63º.

a. A = 71.6°; C = 52.89; b =12.0

C. A = 68.6° C = 45.40; b=12.0

b. A = 71.6°; C = 45.40; b =15.0

d. A = 68.6°; C = 52.89; b=15.0

Answer 1

b. A = 71.6°; C = 45.40°; b =15.0

Explanation:

The missing values can be found with the help of the Law of Cosine and properties of triangles:

Side b (Law of Cosine)

`b = \sqrt{a^(2)+c^(2)-2\cdot a \cdot c \cdot \cos B}`

`b = \sqrt{16^(2)+12^(2)-2\cdot (16)\cdot (12) \cdot \cos 63^(\circ)}`

`b \approx 15.022`

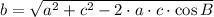
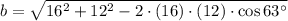
Angle A (Law of Cosine)

`\cos A = -(a^(2) - b^(2)-c^(2))/(2\cdot b \cdot c)`

`\cos A = - (16^(2)-15.022^(2)-12^(2))/(2\cdot (15.022)\cdot (12))`

`\cos A = 0.315`

`A= \cos^(-1) 0.315`

`A \approx 71.639^(\circ)`

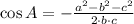
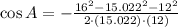
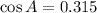
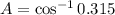
Angle C (Sum of internal angles in triangles)

`C = 180^(\circ) - 63^(\circ) - 71.639^(\circ)`

`C = 45.361^(\circ)`

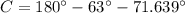
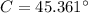
Hence, the right answer is B.