Answer:
B. 6/5, 12/25, 24/125
Explanation:
Let the geometric means to be inserted be x, y and z. The geometric series will contain 5 terms as shown:
3, x, y, z, 48/625
Using the nth term of a geometric sequence to find the missing term.
 where:
where:
a is the first term
n is the number of terms and
r is the common ratio
From the sequence, a = 3
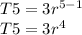
Since the fifth term is 48/625 then:
![3r^(4)=(48)/(625) \\r^(4)= (48)/(625*3) \\r^(4) = (16)/(625) \\r=\sqrt[4]{(16)/(625) } \\r = (2)/(5)](https://img.qammunity.org/2021/formulas/mathematics/high-school/qcsc7hls2llpccf0hzuyj0a7wfkwof77vt.png)
To get the 2nd, 3rd and 4th term, we will substitute the value of the first term and the common ratio in the equation given.

when n = 3;
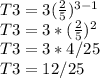
when n = 4;

The three positive geometric mean are 6/5, 12/25, 24/125